Mapping Centrality
The Egyptian symbol for ‘city’, Richard Sennett points out in Conscience of the Eye (p. 46), consisted of a cross bounded by a circle, providing one of the earliest signs of the urban; intersection and enclosure — grid and boundary — come together in this hieroglyph. The notion of the urban as an intersection offers an insight into one of the longest-running themes in urbanism - centrality. Whilst Egyptians made a point of right-angled street intersections, the Roman grid plan (Hippodamus) was designed to explicitly generate centers at different scales, with the earliest phase of settlement locating itself at the intersection of two prominent axial streets, the cardo and the decumanus. To this day cores, hubs, and centers form ever-present concepts in urban discourse; all relate or allude to a set of slippery spatial phenomena we call ‘centrality’.
[ source ]
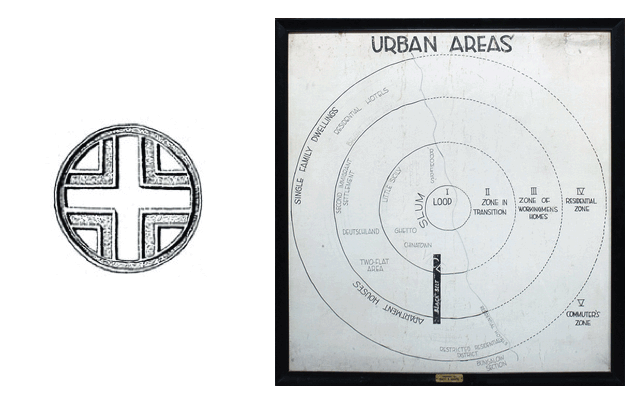
The first formal representation of urban space in modern urbanist discourse was the Chicago School’s concentric model. This updated the Egyptian hieroglyph to the modern metropolis, presenting a symmetrical radial growth emanating from a single Central Business District (CBD), surrounded by successive bands of residential and retail development, an affirmation of centrality as the dominant spatial relation in all matters urban; all space in the urban realm to be defined with respect to a core and a periphery.
In Writings on Cities Lefebvre calls for “a renewed urban society, a renovated centrality”. His essays use varying notions of the concept, providing 35 instances of centrality that present it as intrinsic to the urban, an “essential quality” of its spatial manifestation. “This is the sense of urban centrality, of differences assembled through unity” he states, before moving on to his wish for a “reconstruction of centrality destroyed by a strategy of segregation”. Whilst Lefebvre fractures, diffuses and scatters the concept throughout his texts, in more recent years it has resurfaced in far more precise and quantitative terms than he may have encouraged.
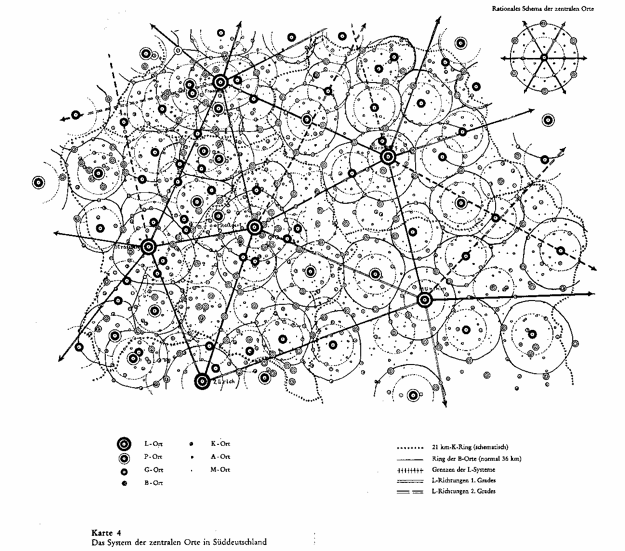
Walter Christaller (1933)
[ more ]
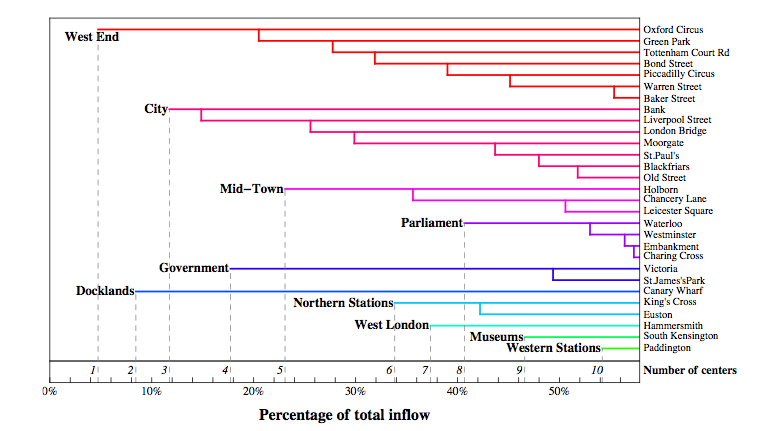
Centrality in modern spatial analysis is strongly tied to graph theoretic measures of nodal relations in topological space. Let us define spatial networks as weighted graphs that use a Cartesian distance or time-based cost function for edge weights. Confining ourselves to such spatial networks we can define closeness centrality as a measure of a node’s closeness in space/time to all the other nodes in a network, and betweenness centrality as a node’s appearance on shortest paths between other nodes, information centrality (Crucitti, 2005) as the impact of node removal on the communicational efficiency of a network, and straightness centrality (Crucitti et al, 2006) as a measure of route efficiency between any two nodes, describing the relation of a straight euclidean path to the actual path on the network. Many other centrality measures can be formulated in this manner. These multiple inter-related centrality phenomena in graphs imply a more complicated tangle of concepts now orbiting the term centrality, focusing on centrality as a function of connectedness.
Roth et Al, 2010
[ source ]
Whilst these forms of centrality are based on dyad relations in a network and can be computed on a node by node basis, they exist in relation to other macroscopic concepts in spatial analysis, namely centricity and centralisation. Centricity can be considered a concept constructed out of a simplifying dualism, monocentrism-polycentrism. This is an axis, or spectrum, describing a multi-scalar phenomenon (local, urban, regional, national, global) which is both functional and morphological (Green, 2007). Centers of activity, centers of population, centers of wealth: Centers are always both relational and functional in nature. Many measures of polycentricity, such as the statistical distribution of sizes of urban settlements, which is often used at the regional scale (Meijers, 2006), focus on just one component of polycentricity, the functional, with no respect for the other, namely the morphology describing the distribution of the centers in space. Centers, to be defined as such, must of course possess a tangible quality, a centrality, which permits them to be distinguished.
Crucitti, Latora, Porta (2006)
[ source ]
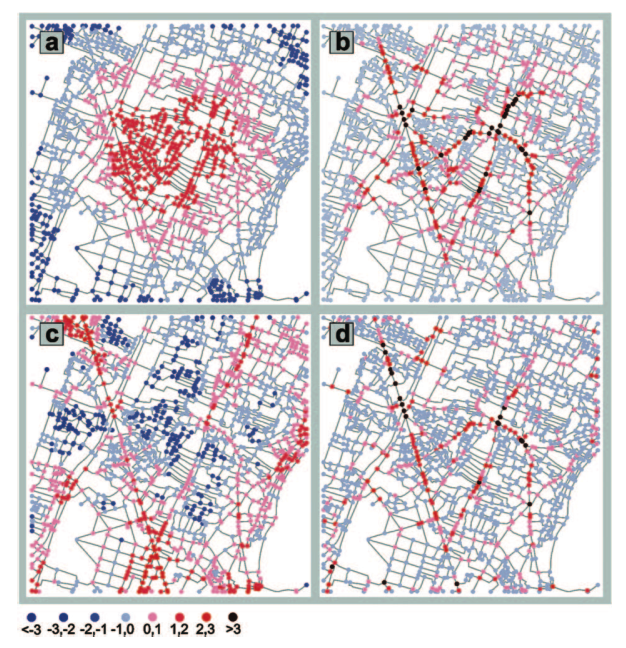
Centralisation, on the other hand, is a measure of spatial concentration, again both in functional and morphological terms. Distributions of activity, population or infrastructure can be examined, their statistical dispersion often giving us insights into how centralised-decentralised a space may or may not be from the point of view of a certain urban activity. Graph theory has its own contributions here: The dispersion of graph theoretic centralities, degree distributions or node assortativity can give insight into the level of centralisation in a spatial system.
Urban modeling has consistently been drawn to centers. Christaller’s Central Place Theory provides a model that produces a hierarchy of increasingly dispersed centers, whilst Wilson’s BLV model, taking ecological dynamics from Lotka-Volterra and entropy maximisation via Boltzmann’s formulation of the microcanonical ensemble, models the slow-scale, complex spatial evolution of centers (e.g. retail). In both these, multiplier, or feedback effects, are present in processes that dynamically produce emergent centers.
Centrality, then, emerges as a strong recurring concept in urban analysis by virtue of its status as a multiple; its ability to not be drawn in to a reductive dualism. There is no one centrality, but one or more centralities, at any given point, in any given spatial system, at any given time.
See Also: Network, archipelago, Boundary, Entropy
Best of the web
- Best Non Gamstop Casinos
- Non Aams Casino 2025
- Betting Sites UK
- Non Gamstop Casinos
- Casinos Not On Gamstop
- Casino Sites Not On Gamstop
- UK Casinos Not On Gamstop
- Migliori Bookmakers Non Aams
- Slots Not On Gamstop
- Non Gamstop Casino Sites UK
- Casinos Not On Gamstop
- UK Casino Not On Gamstop
- Migliori Casino Non Aams
- Casino Sites UK
- Non Gamstop Casinos
- UK Casino Not On Gamstop
- Casinos Not On Gamstop
- Online Slot Sites UK
- Casino Sites Not On Gamstop
- Non Gamstop Casinos UK
- UK Casino Sites Not On Gamstop
- Slots Not On Gamstop
- Slot Online Migliori
- Non Gamstop Casino
- Casino Crypto En Ligne
- Meilleur Casino Belgique
- 씨벳 먹튀
- Malaysia Online Casino